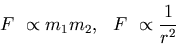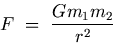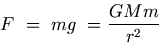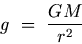Previous Contents Next COLLEGE PHYSICS: GRAVITATION G.1 Introduction From time immemorial, man has been interested in the motion of the heavenly bodies such as the stars, planets and satellites. Many astronomers especially Indian and Arab astronomers have studied these motions in great detail. Among the western scientists, Tyco Brahe and Johan Kepler took a great interest in the motion of planets. Kepler formulated his findings in what are now known as the "Three Laws of Planetary Motion." But the major pioneering work in this field was done by Sir Issac Newton who gave us the Universal Law of Gravitation. G.2 Kepler's Laws From the observations of Tycho Brahe and his own studies, Kepler formulated the laws of planetary motion. The three laws are All planets move in elliptical orbits with the sun at the focus. The radius vector from the sun to the planet sweeps equal areas in equal time. The square of the time period of a planet is proportional to the cube of the semimajor axis of the ellipse. Click here for Solved Example G.1: Time Periods of Satellites G.3 Newton's Law of Gravitation According to Newton's Universal Law of Gravitation, the force of attraction between two point bodies of masses m1 and m2 is directly proportional to the product of the masses and inversely proportional to the square of the distance r between them. This can be mathematically represented as 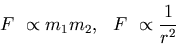(G.1) 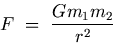(G.2) where G is a proportionality constant called the Universal Gravitation Constant. Its value is 6.67 x 10-11 N m2/kg2. Click here for Solved Example G.2: Gravitational Force of Attraction Click here for Solved Example G.3: Three Stars in a Circular Orbit G.4 Acceleration due to Gravity When a body of mass m falls freely, it is attracted by the Earth (of mass M) with a force F given by Newton's Law of Gravitation. This force is known as Gravity. The acceleration produced by the force of gravity is called acceleration due to gravity and is denoted by g. Using Newton's Second Law of Motion (F = m g) and Newton's Law of Gravitation, we get 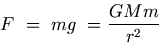(G.3) 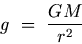(G.4) Equation (G.4) thus gives the expression for acceleration due to gravity. Note that this acceleration is independent of the mass of the body itself. The value of g is typically taken to be 9.8 m/s2. Click here for Solved Example G.4: Acceleration on Other Planets   Previous Contents Next

 

English
Français
Português
Español
Deutsch
日本語
हिन्दी