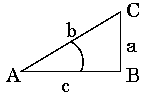Math : Trigonometry

• Values of Trigonometric Functions for Common Angles
  

   

• Important Trigonometric Identities
  

   

• Cofunction Property

Values of Trigonometric Functions for Common Angles

It is possible to obtain the values in the above table for 0, 45^o and 90^o by using the definitions from Trigonometry Module 1.

The values in the above table can be easily remembered using the following mnemonic. The values of sin 0, sin 30^o, sin 45^o, sin 60^o and sin 90^o are simply given by the square roots of 0/4, 1/4, 2/4, 3/4 and 4/4. The values of cos 0, cos 30^o, cos 45^o, cos 60^o and cos 90^o are given by the square roots of 4/4, 3/4, 2/4, 1/4 and 0/4. Obviously, the values of tan for any angle are obtained by dividing the sine value by the cosine value.

Important Trigonometric Identities

Some important trigonometric identities relating functions of a single angle (say, A) are given below.

These identities are useful in simplification and solution of problems. Their proofs are given below.

• Based on the right-angled triangle in the figure alongside, sin A = a / b and cos A = c / b.
  Therefore sin² A + cos² A = (a² + c²)/b².
  By Pythagoras Theorem, a² + c² = b² in a right-angled triangle.
  Thus sin² A + cos² A = 1 and equation (1) is proved.

   

• On dividing both sides of equation (1) by cos² A,
  we obtain tan² A + 1 = 1 / cos² A = sec² A. Equation (2) is proved.

   

• On dividing both sides of equation (1) by sin² A,
  we obtain 1 + cot² A = 1/sin² A = cosec² A. Equation (3) is proved.

Cofunction Property

The cofunction property is easy to prove by starting with the fact that the sum of the three angles of a triangle is always 180^o, i.e., A + B + C = 180^o. For a right-angled triangle, angle B is 90^o and A + C = 90^o. On using 90^o - C = A, the following are readily obtained:

• sin (90^o - A) = sin C = c / b = cos A
• cos (90^o - A) = cos C = a / b = sin A
• tan (90^o - A) = tan C = c / a = cot A