Heat transfer problem solution BSL : Maximum current in an electric wire

Heat Transfer Problem :
Maximum current in an electric wire

Problem.

An electric wire with radius r₀ of 0.5 mm is made of copper [electrical conductivity = 5.1 x 10⁷ ohm^-1 m^-1 and thermal conductivity = 380 W/(m K)]. It is insulated (see figure) to an outer radius r₁ of 1.5 mm with plastic [thermal conductivity = 0.35 W/(m K)].

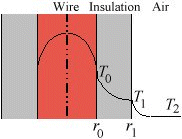
Figure. Heating of an insulated electric wire.

The ambient air is at 38^oC and the heat transfer coefficient from the outer insulated surface to the surrounding air is 8.5 W/(m² K). Determine the maximum current in amperes that can flow at steady-state in the wire without any portion of the insulation getting heated above its maximum allowable temperature of 93^oC.

Solution.

In general, the heat flow is given by Q = T/R_th, where T is the temperature driving force (thermal potential difference). The thermal resistance for a cylindrical annulus is R_th = ln (r₁/r₀)/(2kL) and the thermal resistance for a fluid film at a solid-fluid interface is R_th = 1/(hA). Here, k is the thermal conductivity, h is the heat transfer coefficient and A is the surface area for convection.

The thermal resistances for the insulation and air film are in series as shown in the figure below.

Figure. Thermal resistance representation of insulation and air film.

Based on the above thermal resistance representation, the heat flow is

(1)

where k is the thermal conductivity of the plastic insulation.

The flow of an electric current results in some electrical energy getting converted to thermal energy irreversibly. The heat generation by electrical dissipation per unit volume is given by S = I ²/k_e where I is the current density (in amp/m²) and k_e is the electrical conductivity (in ohm^-1 m^-1).

The total heat generated within the wire is simply the product of S and the volume of the wire. At steady-state, all this heat generated within the wire by electrical dissipation must leave through the wire surface and therefore the heat flow is given by

On multiplying the current density by the cross-sectional area of the wire, the current is obtained from

On setting the temperature T₀ to 93^oC (i.e., the maximum allowable temperature for the insulation), substitution of the numerical values gives the maximum current that can flow through the wire as

Heat Transfer Problem : Maximum current in an electric wire

Heat Transfer Problem :
Maximum current in an electric wire