Heat transfer problem solution BSL : Minimum thickness for a composite furnace wall

Heat Transfer Problem :
Minimum thickness for a composite furnace wall

Problem.

The wall of a furnace comprises three layers as shown in the figure. The first layer is refractory (whose maximum allowable temperature is 1400^oC) while the second layer is insulation (whose maximum allowable temperature is 1093^oC). The third layer is a plate of 6.35 mm thickness of steel [thermal conductivity = 45 W/(m K)]. Assume the layers to be in very good thermal contact.

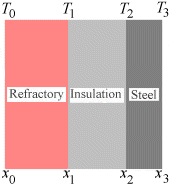
Figure. Layers in a composite furnace wall.

The temperature T₀ on the inside of the refractory is 1370^oC, while the temperature T₃ on the outside of the steel plate is 37.8^oC. The heat loss through the furnace wall is expected to be 15800 W/m². Determine the thickness of refractory and insulation that results in the minimum total thickness of the wall.

Given thermal conductivities in W/(m K):

Layer k at 37.8^oC k at 1093^oC

Refractory 3.12 6.23

Insulation 1.56 3.12

Solution.

In general, the heat flow is given by Q = T/R_th and the thermal resistance for a rectangular slab is R_th = x/(kA), where T is the temperature driving force (thermal potential difference), x is the slab thickness, k is the thermal conductivity, and A is the cross-sectional area of the slab.

The thermal resistances for the three layers are in series as shown in the figure below.

Figure. Thermal resistance representation of composite furnace wall.

Based on the thermal resistance representation for the composite furnace wall, the heat flux q is

$equation : q = Q/A = (T_0 - T_1)/[(x_1 - x_0)/k_{01}]$

(1)

In the refractory and insulation, the thermal conductivity k varies with temperature. If a linear variation is assumed, then the arithmetic mean is to be used for the thermal conductivity.

The temperature T₂ at the interface between the insulation and steel layers is given by

Since q, T₀ and T₂ are known in the above expression, the first two terms on the right-hand side are nearly fixed. The last term is negative as k₁₂ is less than k₀₁ (i.e., thermal conductivity of insulation is less than that of refractory). Since the aim is to minimize (x₂ - x₀), the temperature T₁ must be maximized.

Next, the temperature T₁ is set to 1093^oC (i.e., the maximum allowable temperature for the insulation). By linear extrapolation, the thermal conductivity of the refractory at 1370^oC is 7.05 W/(m K). Substitution of numerical values gives the thickness of refractory as

Layer	k at 37.8^oC	k at 1093^oC
Refractory	3.12	6.23
Insulation	1.56	3.12

Heat Transfer Problem : Minimum thickness for a composite furnace wall

Heat Transfer Problem :
Minimum thickness for a composite furnace wall