Heat transfer problem solution BSL : Maximum temperature in lubricant by viscous heating

Heat Transfer Problem :
Maximum temperature in lubricant by viscous heating

Problem.

An oil (of viscosity and thermal conductivity k) acts as a lubricant between two coaxial cylinders. The inner cylinder is stationary and the outer cylinder of radius R rotates at an angular velocity . The clearance between the cylinders is b, which is small compared to the radii of the cylinders; so, curvature effects can be neglected and the cylindrical system can be approximated by a plane narrow slit (to be solved in Cartesian coordinates) as shown in the figure. Derive an expression for the maximum temperature in the lubricant if both cylinders are at temperature T₀. Neglect the temperature dependence of and k, but explicitly take into account the heat generated by viscous dissipation.

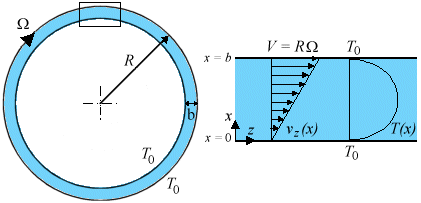
figure : coaxial cylinders approximated by plane narrow slit

Figure. Temperature profile for viscous heat generation. The rectangular section in the flow between two coaxial cylinders can be approximated by the plane narrow slit on neglecting the curvature of the bounding surfaces.

Solution.

The clearance between the cylinders is b, which is small compared to the radii of the cylinders; so, curvature effects are neglected and the cylindrical system is approximated by a plane narrow slit. From a shell momentum balance in Cartesian coordinates over a thin rectangular slab of thickness x, the momentum flux (shear stress) distribution is obtained as

$equation : d tau_{xz}/dx = Delta P / L = 0 implies tau_{xz} = K_1$

(1)

The flow is solely due to the movement of the top surface and there is no pressure gradient imposed on the system.

On substituting Newton's law of viscosity ( $equation : tau_{xz} = -mu dv_z/dx$ ), the expression for the velocity profile is

(2)

The integration constants K₁ and K₂ are determined using the boundary conditions:

(3)

(4)

On substituting the integration constants, the velocity profile is given by

(5)

During viscous flow, fluid layers rub against adjacent layers of fluid and the internal friction produces heat. In other words, mechanical energy is degraded into thermal energy irreversibly. The heat generation by viscous dissipation per unit volume depends on the local velocity gradient and is given by

At steady-state, the accumulation term is zero. From a thermal energy balance over a thin rectangular slab of thickness

x in the fluid, we get

where A is the cross-sectional area of the narrow slit and q_x is the heat flux for conduction in the x-direction.

The integration constants C₁ and C₂ are determined using the boundary conditions:

Thus, the maximum temperature occurs at the mid-plane of the slit and is obtained as

Heat Transfer Problem : Maximum temperature in lubricant by viscous heating

Heat Transfer Problem :
Maximum temperature in lubricant by viscous heating